«Угадай расстояние»
Подготовка. В эту игру можно играть и на улице, и дома, в очереди на почте или в магазине. Никакой подготовки и реквизита не нужно.
Правила. Выбираем цель. Например, это елка. И спрашиваем ребенка: «Сколько шагов от меня до елочки?» При этом мы изначально договариваемся, какими шагами считаем: «гигантскими», «лилипутскими», «прыжками». Высказываем гипотезу: «Я думаю, что от меня до елочки столько-то гигантских шагов, столько-то прыжков». Взрослый называет вслух свою версию, а потом пробует, проверяет гипотезу. А потом предлагаем ребенку выбрать новую цель, угадать до нее расстояние в лилипутских шагах, а в следующий раз — в прыжках. А если мы хотим усложнить задачу, то просим ребенка сразу использовать обязательно два типа шагов, например, зонтики и великаны. Ну, а потом проверяем эту гипотезу на практике.
Игра с кубиками
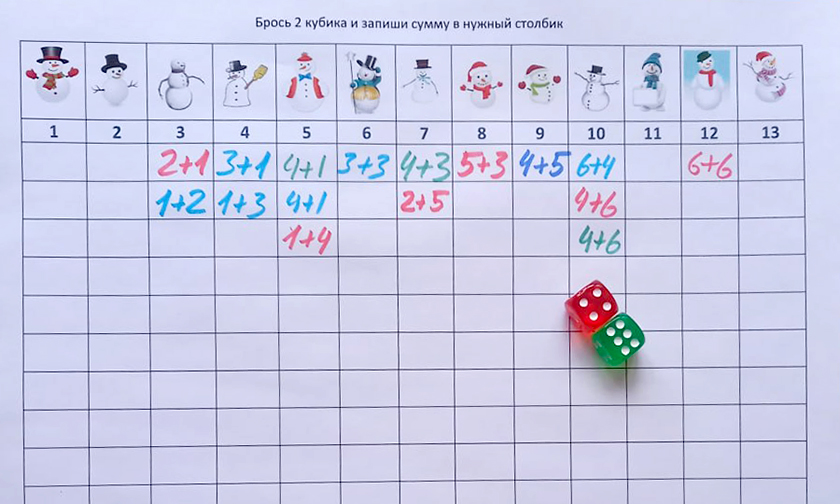
Подготовка. Чертим таблицу или распечатываем с сайта. Вверху рисуем 14 снеговиков, каждому присваиваем номер. Под ними рисуем 10 строчек.
Правила. Первый игрок кидает два кубика и считает сумму. Например, на кубиках выпало 3 и 5. Сумма — 8. Пишем под снеговиком №8 эту сумму (3+5). Снеговик сдвинулся на один шаг.
Следующий кидает кубики. Выпало — 4 и 4. Снеговик №8 сдвинулся еще на шаг. Вопрос — какой снеговик дойдет первым до финиша?
Плюсы. Это игра на теорию вероятностей. Иногда и взрослым не сразу бывает очевидно, какой из снеговиков с наибольшей вероятностью выиграет. Но ценность игры не только в этом. В какой-то момент ребенок говорит: «А ведь снеговик №1 не выиграет, зря его написали». И это важный момент, о котором полезно поговорить с детьми. Мало заметить это, хорошо бы еще и суметь объяснить, отчего ты так думаешь… И многие дети вполне разумно отвечают: «Смотри, у нас ведь кубиков два. Самое маленькое число, которое может выпасть — это 2 (1+1). Значит, первый снеговик просто не может выиграть!»
В какой-то момент ребенок понимает, что снеговик №13 и снеговик №14 тоже не сдвинутся с места. Потому что максимальное выпавшее число может быть только 12, если на обоих кубиках выпадет по 6. И эта несложная на вид игра стоит того, чтобы ребенок задумался и сформулировал это.
Крестики-нолики с игральными кубиками
Подготовка. Рисуем поле (можно самим, а можно скачать на сайте «Мышематики»). На поле пишем вразнобой числа от 2 до 12 в разных клетках. Какие-то числа должны повторяться, при этом мы пишем на поле больше шестерок, семерок и восьмерок, чем 2 и 12. После этого мы берем два игральных кубика и два фломастера разного цвета — для двух игроков.
Правила. Первый игрок кидает два кубика, считает сумму чисел, которые выпали. Например, на кубиках выпали числа 3 и 4. Игрок ищет на числовом поле сумму — 7. И ставит крестик на этой клетке.
Второй игрок берет свои два кубика, кидает их, считает выпавшую сумму. Например, это 11. Ищет 11 на поле. Ставит нолик.
Кто выстроит в ряд четыре крестика или четыре нолика по горизонтали или вертикали, тот и выиграл.
Варианты игры. Есть похожее поле, уже на тему «умножение». Там аналогичные правила игры, только мы не складываем, а умножаем числа, которые выпали на кубиках. Скачать поле можно вот тут.
Плюсы. С одной стороны, есть кубики, которые каждый раз выдают непредсказуемый результат. С другой — игрок строит свою стратегию, и перед каждым ходом ему надо непременно решить, что лучше делать на этот раз — поставить крестик для выстраивания линии для себя или крестик, чтобы помешать второму игроку. Дети обычно увлекаются этой игрой и готовы сыграть несколько партий подряд, они пробуют разные стратегии и хотят применить свои идеи в следующий раз.
Тетрамино
Подготовка. Каждый рисует себе квадрат со сторонами шесть на шесть клеток и все фигуры тетрамино — квадрат из четырех клеток, потом две триминошки, доминошку и однушку. А дальше мы договариваемся, какие поля будут запретными. Ставим крестики на них. В обоих квадратах эти поля должны быть, конечно же, одинаковыми.
Каждую игру запретные поля могут быть по-разному расположены. Например А1 и А6, Б2 и С5. Всего запретных полей должно быть семь. Эти запретные поля не могут отгораживать какие-то клетки и «отрезать» их от остального поля.
Правила. После этого каждый игрок размещает все свои фигурки на поле. Количество клеток такое, что все фигурки должны разместиться.
Получается, что кто-то быстрее сможет расположить фигуры на поле. Тогда можно дать фору медленному игроку — разрешить ему переносить одну запретную фишку, куда ему захочется.
Вырезание снежинок
Вырезание снежинок — это сплошная математика. Для того, чтобы вырезать окошко нужной формы, надо понимать, как нарисовать половину этой фигуры на сгибе. Можно вырезать из бумаги маски, хороводы, снежинки с четырьмя или шестью лучами, можно делать бумажных зверей или комнатку из листа бумаги.
Если хотите задачу посложнее, можете сделать из бумаги фрактал, или снежинку-хоровод, снежинку с шестью лучами. Можно скачать готовые шаблоны и вырезать снежинки по ним, но куда интереснее попытаться понять самому, как сложить и что вырезать, чтобы именно такая снежинка получилась.
Шаблоны снежинок можно скачать тут.
Начинаем с самого простого — как сложить лист бумаги и как вырезать окошко на сгибе. Мы можем сложить листок пополам и на сгибе вырезать треугольник. В качестве первой вводной задачи давайте введем такое ограничение — что мы умеем вырезать только треугольники. А теперь вопрос: какой формы окошки у нас могут получиться и сколько разных ответов у этой задачи?
Обычно говорят — ромбик получится. Это верно, но это не единственный ответ. Потом называют квадрат.
А что еще можно вырезать? В этот момент взрослые и дети зависают одинаково. А на самом деле там еще много разных четырехугольников, которые можно получить, если мы умеем вырезать только треугольник.

После этого мы вырезаем маску. Нужно понять, как сложить листочек, чтобы вырезать рот и два глаза. Взрослым обычно кажется, что это очень просто. Однако многие дети начинают с того, что вырезают рот на краях, а не на сгибе. А потом надо придумать, как вырезать глаза. Ребенок должен сам понять, как получить симметричные отверстия.
Как сделать так, чтобы глаза были на одинаковом расстоянии от центра? Взрослым кажется, что это простая задача, потому что у них было больше практики с ножницами.
Если взрослым хватит терпения не подсказать, не продиктовать, что и как резать, то дети смогут сами додуматься. Самое лучшее, что могут сделать взрослые, когда обнаружат, что дети резали не то и не там — просто подать следующий листок ребенку, чтобы он мог продолжить эксперименты. Нужно просто подождать и дать самому проверить разные гипотезы.
Хоровод
Другая красивая идея из серии «Математика с ножницами» — гирлянда или хоровод. Берем полоску бумаги, складываем в гармошку. Вопрос — как из этой гармошки сделать бумажный хоровод? Как сложить листок и что вырезать, чтобы получились человечки, которые держатся за руки?
Кажется, что это простая задача. Но многим детям совсем не очевидно, как резать так, чтобы человечки не распались на отдельные фигурки, а держались за руки.
Можно затем предложить усложнить задание. Сделать хоровод с чередующимися фигурками — котик-елочка-котик-елочка. Возможно, ребенок изрежет не один лист, пока поймет, как это сделать. Это настоящий эксперимент, который ребенок обдумывает, выполняет и понимает, как нужно все сложить и вырезать.
Одним разрезом вырезать букву «П»
У всех этих экспериментов с бумагой, ножницами и снежинками есть математическое продолжение. Существует теорема об одном разрезе.
Эту теорему доказал молодой математик Эрик Демейн. По-английски эта теорема называется «Fold-and-cut theorem». В ней говорится, что всегда можно так сложить лист бумаги, что любой многоугольник, нарисованный на нем, будет вырезаться одним прямолинейным разрезом.
Можно вырезать елочку, конфету, букву, рыбку. Сделав только один разрез в сложенном листе бумаги.
Как пролезть через листок бумаги формата А4. Неужели это возможно?
Весьма вероятно, что вы в детстве встречали подобный фокус, но если нет, то посмотрите сами, как это сделать.
В качестве подготовительного шага даем детям листочек и говорим, что мы можем прорезать в этом листе такую хитрую дырку, что сможем потом пролезть через нее. «Не может быть», — говорит ребенок. «Попробуй сам», — говорим мы.
Тогда мы даем подсказку. Берем узкую полоску бумаги, например, лист А4 разрезаем пополам. И надрезаем снизу как расческу этот лист, получается бахрома. После этого сверху, в противофазе, тоже надрезаем лист, как будто у нас одна расческа снизу, а вторая сверху, со сдвигом. После чего берем за края, тянем в сторону.
Полоска бумаги, надрезанная сверху и снизу, удлиняется и растягивается очень сильно. И эта подсказка поможет ребенку понять, как разрезать лист бумаги для того, чтобы пролезть через это окошко. Возможно, вы сможете так аккуратно надрезать лист, что пролезете в окошко вдвоем или втроем.
Математика — это красиво и не страшно. Можно выбирать те части математики, которые вас радуют больше всего: вырезать из бумаги симметричные открытки, рисовать фракталы, играть в головоломки типа тетрамино, устраивать гонки снеговиков.
Фото предоставлены Женей Кац